你知不知道，当你每次在喜刷刷的刷屏一拉到底的时候，都在用格拉姆施密特正交化方法进行矩阵的QR分解？

作为许多年以前线性代数六十几分低空飘过的数学渣渣，再次见到这些熟悉而又陌生单词，我不禁感到蛋蛋的忧伤。没想到这辈子还能遇到这玩意儿-_-!

在手机上用手指划屏幕进行滚动的时候，手指离开后，页面还是会往下滚一会儿。手指划的越快，继续滚的距离也就越多。在Chrome里是这样实现的，一系列的touch事件记录下来，包括时间和位置，然后就能求得划动的速度，手指离开速度慢慢衰减到零。

这个速度怎么算呢，默认的策略是用最小二乘法进行二次多项式拟合。拟合这一系列的 (时间t, 位置d) 数据，使 ||d - (a + bt + ct^2)|| 最小。具体怎么算，就是用开头的那个东西啦。鉴于本人数学学渣，在此略过不表……

不过，虽然本人数学学渣，但这毕竟只是个二次方程嘛。我初中什么样的二次方程没见过？不知道比这个高到哪里去了！于是本人当时就画了一个图，用这样的数据，你用二次多项式给我拟合一个看看！

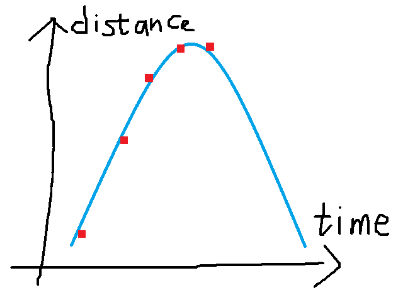
LSQ approximation

如图所示，手指快速滑动屏幕，然后快速停下，然后才离开屏幕。用这样的输入数据，拟合得到的手指离开时的速度正好与我们手指滑动的方向相反，于是手指离开屏幕的时候，屏幕就会又相反方向滑了。(快速停下与手指离开屏幕之间时间间隔需小于80毫秒)

经验证，Chrome安卓版可以实现这样的效果。Chrome这一块抄了安卓代码，安卓系统里也是这样的效果。